Using the PostgreSQL Recursive CTE – Part Two
Computing Bacon Numbers for actors listed in the IMDb
YugabyteDB is an open source, high-performance distributed SQL database built on a scalable and fault-tolerant design inspired by Google Spanner. YugabyteDB uses its own special distributed document store called DocDB. But it provides SQL and stored procedure functionality by re-using the “upper half” of the standard PostgreSQL source code. This is explained in the two part blog post “Distributed PostgreSQL on a Google Spanner Architecture”: (1) Storage Layer; and (2) Query Layer.
This is the second of a two-part blog series. Part One is Traversing an employee hierarchy. Each of these case studies, the employee hierarchy and the Bacon Numbers problem, is a famous example of the use of the PostgreSQL recursive CTE. Because YugabyteDB re-uses the PostgreSQL SQL processing code “as is” (see the Query Layer post), everything that I say in the present two-part blog post series applies in the same way to PostgreSQL as it does to YugabyteDB. In particular, all the code has the identical effect in the two environments. I hope, therefore, that developers who mainly use only PostgreSQL, as well as YugabyteDB aficionados, will find these posts interesting.
Because a hierarchy is the most restrictive kind of graph, Part One used a simple representation and a simple traversal method. The Bacon Numbers problem is based on the most general kind of graph—an undirected cyclic graph. Part Two therefore uses the general graph representation and the general traversal method.
I recently finished writing a thorough treatment of the WITH clause in YugabyteDB’s YSQL documentation in this dedicated section:
The WITH clause and common table expressions
It includes this dedicated subsection:
I’ll link extensively to explanations and especially to code examples in my account in the YSQL documentation so that, in these two posts, I can focus on the high-level narrative and make them as short as possible. I included full accounts of the two case studies that these posts describe in the YSQL documentation here:
Using a recursive CTE to traverse an employee hierarchy
and here:
Using a recursive CTE to compute Bacon Numbers for actors listed in the IMDb
All the code snippets and pictures in this post are copied from the YSQL documentation. The main page of the overall WITH clause and common table expressions section explains that all the code is available in a downloadable code zip with a few master scripts to run all of the code mechanically.
The following note is copied from Part One:
Note: You often hear the term “recursive WITH clause” in place of “recursive CTE”. (I spelled it out here so that readers might find this blog post using Internet search.) This usage is erroneous. A whole WITH clause can’t be described as “recursive” or not. Rather, just a single CTE (and only the first one) can be so described. However, the mistake is widespread (as Internet search will show you) and seems never to lead to misunderstanding.
What is the Bacon Numbers problem?
There’s a nice account of the Bacon Numbers problem in the Wikipedia article Six Degrees of Kevin Bacon. The central idea is that Kevin Bacon has acted in so many famous movies that, considering all of them together, he’ll have acted with many famous co-actors. Then, by extension of this thinking, each of these co-actors, over the span of their careers, will have acted with other co-actors—some of whom will never have acted with Kevin Bacon. And so it goes on. Such a chain of connection will extend until: either it reaches an actor who was a one-movie-wonder; or it reaches an actor who has already been reached from Bacon by a shorter chain. An actor’s Bacon Number is the length of the shortest chain connecting them to Kevin Bacon. Here’s the full answer to the question “What is Al Pacino’s Bacon Number?”
Kevin Bacon She's Having a Baby Wild Things Bill Murray Saturday Night Live: Game Show Parodies Billy Crystal Muhammad Ali: Through the Eyes of the World James Earl Jones Looking for Richar Al Pacino
The actors are rendered in a boldface font. And the common movies between an adjacent pair of actors are rendered in an italic font. So Al Pacino’s Bacon Number is four, James Earl Jones’s number is three, Billy Crystal’s number is two, and Bill Murray’s number is one. As you’ll see by the end of this post, the chain shown above is the real ysqlsh output from real SQL embedded in a real PL/pgSQL table function, acting on real IMDb data.
The Bacon Numbers problem is popular as an assignment for Computer Science classes. See, for example, the Oberlin College Computer Science Department’s assignment “Everything is better with Bacon”. This one asks for a solution written in Java. Then there’s the University of Washington Computer Science & Engineering Department’s Assignment 1: SQL Queries… This one specifically wants a solution that uses PostgreSQL. But the “solution” link leads to a password-protected page. No amount of Internet searching took me to even a single example of a self-contained working SQL solution that you could run on actual data—never mind which SQL database it used. But I got lots of irrelevant hits for solutions that use NoSQL or Graph databases.
Ascending from the particular to the general—and descending back down to the particular
If you’re reading this post, then the chances are that you’ve already had a fair exposure to graphs:
- the terms of art with which you discuss their structural elements (nodes, edges, and the attributes that occurrences of these two element types might have);
- graph taxonomy (undirected cyclic graph, directed cyclic graph, directed acyclic graph, and rooted tree);
- and maybe, too, algorithms for finding paths.
The taxonomy is summarized pictorially in the YSQL documentation section Using a recursive CTE to traverse graphs of all kinds within the overall WITH clause section. Here is an undirected cyclic graph:
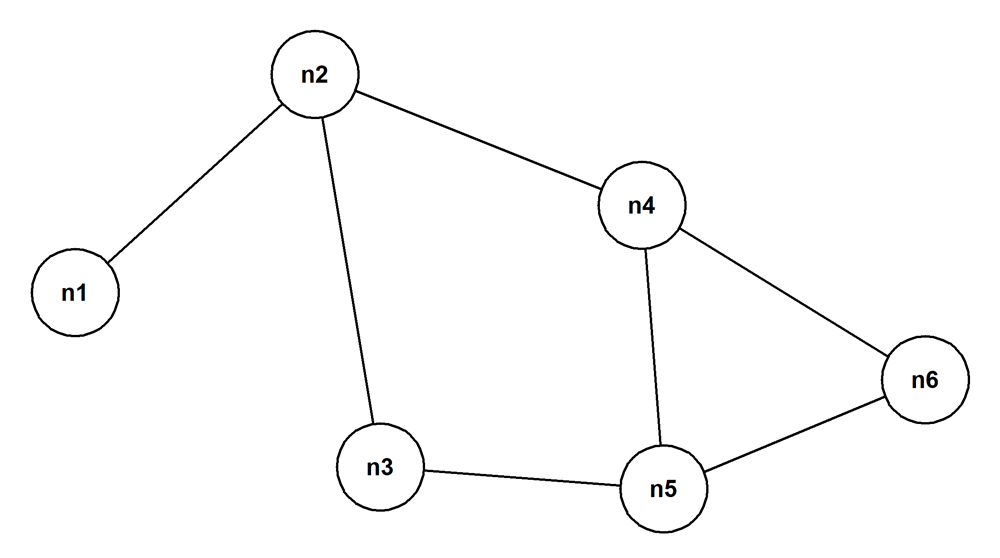
The Bacon Numbers problem is set against this kind of graph. The nodes are the actors. And an edge exists between a pair of actors when they’ve both acted in at least one movie together. The relationship between a pair of actors is symmetrical: they’re simply peers. Contrast this with the asymmetry of the relationship between a manager and the employees who report to them.
You can exercise a fair amount of pragmatic freedom of choice when you decide how to represent the data that the solution to the Bacon Numbers problem depends on in a SQL database. I address these freedoms, in the general domain, in the YSQL documentation section Representing different kinds of graph in a SQL database. For reasons that I explain there, I decided to use a representation where each edge is represented twice—once in each direction. I describe this, and the path finding SQL that goes with it in the subsection Graph traversal using the denormalized “edges” table design in the section Finding the paths in a general undirected cyclic graph.
You might think that this scheme is crazy—especially when you compare it with the second scheme, described in the subsection Graph traversal using the normalized “edges” table design, where each edge is represented just once. But, as I explain there, the SQL is very much simpler, and more performant, for the “denormalized edges” representation than for the “normalized edges” representation.
Notice that all that’s needed to support path finding is the “edges” table with columns for the node ID at each of its ends. Path finding needs only to know about the existence of edges and doesn’t care about what properties they might have. However, in the bigger picture, when it comes to showing a result like I do for the connection between Kevin Bacon and Al Pacino at the start of this post, you need to know what movies brought each edge. This is done conveniently by giving the “edges” table a “movies” column. This column represents a multivalued attribute: the list of movies, as a text[] array, that the pair of actors at the end of an edge have been in together. Codd and Date devotees might feel uneasy about this. But if you study the implementation that the section Decorate the path edges with the list of movies that brought each edge explains, then you’ll see that the departure from strict normal form makes the coding simple and clear.
Create the table like this to represent the graph shown above:
create table edges( node_1 text not null, node_2 text not null, constraint edges_pk primary key(node_1, node_2)); alter table edges add constraint edges_chk check(node_1 <> node_2);
Step through the code blocks at the start of the section Using a recursive CTE to traverse graphs of all kinds to insert the rows, see them, and test that some key constraints hold. You’ll see immediately that, for example and as promised, the single edge in the picture above between the nodes “n2” and “n4” is represented twice: both as “n2 > n4” and as “n4 > n2”. In other words, the table actually represents a constrained kind of directed cyclic graph where every connected node pair is joined by two edges—one in each direction.
Because the treatment in the whole of the parent section, Using a recursive CTE to traverse graphs of all kinds, is use-case agnostic, the “edges” table has columns called “node_1” and “node_2” rather than “actor_1” and “actor_2”.
The next section describes the path finding scheme (staying at the general, use-case agnostic level) and compares it with the corresponding scheme for the employee hierarchy use case that Part One of this two-part series addressed. But before that, I’ll descend briefly again to the particular, as promised, to mention another much-loved formulation of the Bacon Numbers problem. It’s described in the Wikipedia article Erdős number. Briefly, the “actor” node becomes the “mathematician” node, the “movies list” edge becomes the “published mathematical papers” list edge, and “Kevin Bacon” becomes renowned Hungarian mathematician “Paul Erdős”. From the point of view of the SQL programmer, this trivial re-spelling of the Bacon Number problem, itself a dramatised formulation of the general problem to find paths in an undirected cyclic graph, couldn’t be less interesting. But for serious mathematicians with a penchant for pub quizzes, it couldn’t be more germain. Believe it or not, the business gets yet more nerdy. Look at the Wikipedia article Erdős–Bacon Number. It goes on yet further to talk about the Erdős–Bacon-Sabbath Number. This includes the Sabbath Number, an equivalent to the Bacon Number that connects musicians to the band Black Sabbath!
Comparing the approach for finding paths in a hierarchy to the approach for finding paths in an undirected cyclic graph
Look first at the core of the code that finds the paths in the employee hierarchy that was the focus of Part One. The full code is presented for copy-and-pasting into ysqlsh at the code block cr-view-top-down-paths.sql in the section List the path top-down from the ultimate manager to each employee in breadth first order. In the extract below, the various names have been generalized from the specific domain of a workplace’s organization structure to the agnostic domain of a hierarchy of nodes:
emps > nodes [the alias] e > n emps.name > nodes.node_id emps.mgr_name > nodes.parent_node_id
This is the code that results:
with recursive paths(path) as ( -- Non-recursive term ( select array[node_id] -- SPECIFIC TO from nodes -- HIERARCHY where parent_node_id is null -- " ) union all -- Recursive term ( select p.path||n.node_id -- " from nodes as n -- " inner join paths as p -- " on n.parent_node_id = p.path[cardinality(path)] -- " ) ) select path from paths;
Notice how the array concatenation operator || is used to extend the path by one element at each successive repeat of the recursive term. Array functionality comes to the rescue, as we shall see, several times in the code that the solution to the Bacon Numbers problem relies upon.
The prose account of how this works, in Part One, is generalized here thus:
The non-recursive term starts from the root node of the rooted tree (i.e. the node whose “parent_node_id” column, uniquely, is NULL) and finds all its children. Then, the first repetition of the recursive term starts with the root node’s children and, for each, finds its children. And so it goes on: each repetition of the recursive term goes one level deeper down the hierarchy—often, early on, producing more results each time than the previous time, reflecting the fact that trees are often bushy. At each step, the path upwards from a just-added node all the way to the root node is available (if only you care to write the logic to maintain this path in the SQL that defines the recursive term). Eventually, each repetition of the recursive term starts to produce more and more childless nodes and correspondingly fewer and fewer nodes with children—so that each repetition now produces fewer results than the previous one. It all stops when the repetition produces only childless nodes because the next repetition looks for the children of these childless nodes—and tautologically there aren’t any.
Here, now, is the corresponding code that finds the paths in an undirected cyclic graph. It’s presented copy-and-paste ready for you to try on the graph whose ”edges” table you’ve already populated—provided that you followed the link to the section Graph traversal using the denormalized “edges” table design in the YSQL documentation and ran the code blocks for setting up the data that it presents.
deallocate all; prepare stmt(text) as with recursive paths(path) as ( -- Non-recursive term ( select array[$1, node_2] -- SPECIFIC TO from edges -- UNDIRECTED where node_1 = $1 -- CYCLIC GRAPH ) union all -- Recursive term ( select p.path||e.node_2 -- " from edges e -- " inner join paths p -- " on e.node_1 = p.path[cardinality(path)] -- " -- " -- Prevent cycles. -- " where not e.node_2 = any(p.path) -- " ) ) select path from paths;
The predicate “not e.node_2 = any(p.path)” is essential. It refuses to make a new path by extending an existing path that results from the previous repetition of the recursive term if the next step would reach a node that is already on the to-be-extended path. (Of course, as just a special case, this test prevents going back to the starting node.) Prepare and execute “stmt()” without the cycle-prevention test. You see that it goes on forever until you interrupt it with ctrl-C.
Once again, “array” functionality comes to the rescue! Check out the account of the ANY array operator in the YSQL documentation.
The very striking similarity between the recursive CTE for finding the paths in a hierarchy and the CTE for finding the paths in an undirected cyclic graph is due to the “trick” of representing each edge for the latter in both directions. This means that the next node is always found by looking for one whose “node_1” value is equal to the “node_2” value for the previous node in just the same way that the next node in a hierarchy is found by looking for one whose “parent_node_id” value is equal to the “node_id” value for the previous node. As mentioned, without this trick, the recursive CTE for path finding in an undirected cyclic graph becomes rather tortuous, and the striking similarity with the approach for a hierarchy is lost. See the section Graph traversal using the normalized “edges” table design in the YSQL documentation.
Here’s the prose narrative, “translated” from the narrative for the employee hierarchy. The non-recursive term starts from whichever node you choose and finds all the nodes connected directly to it via an edge. Then, the first repetition of the recursive term starts with the nodes that are immediately connected to the starting node and, for each, finds the nodes that are immediately connected to it. However, and this is critical:
it’s possible that one or more of these newly reached nodes have already been reached by a shorter path under a previous repetition—and such a node must not be added to the growing ultimate result set.
And so it goes on: each repetition of the recursive term goes one path step further away from the starting node—often, early on, producing more results each time than the previous time, reflecting the fact that each node is usually immediately connected to many others. At each step, the path back from a just-added node all the way to the starting node is available (if only you care to write the logic to maintain this path in the SQL that defines the recursive term).
Eventually, result set growth changes to result set shrinkage with each next repetition. More and more “dead end” nodes are unioned into the growing result set. (A “dead end” node is one from which other edges that terminate at it lead only to nodes that have already been encountered.) Correspondingly, fewer and fewer nodes are added from which paths can be followed to nodes that haven’t yet been found. (The case that you reach a node that can be reached only by the path you just traversed to reach it is simply a special case of this more general stopping condition. This is how backtracking is prevented.) This means that, sooner or later, each next repetition of the recursive term produces fewer and fewer nodes from which unencountered nodes can be reached than the previous repetition. It all stops when the repetition produces only nodes from which there’s nowhere new to travel.
Test the prepared statement like this:
execute stmt('n1');This is the result:
path
---------------------
{n1,n2}
{n1,n2,n3}
{n1,n2,n4}
{n1,n2,n4,n5}
{n1,n2,n4,n6}
{n1,n2,n3,n5}
{n1,n2,n4,n5,n3}
{n1,n2,n3,n5,n4}
{n1,n2,n3,n5,n6}
{n1,n2,n4,n5,n6}
{n1,n2,n4,n6,n5}
{n1,n2,n4,n6,n5,n3}
{n1,n2,n3,n5,n4,n6}
{n1,n2,n3,n5,n6,n4}I added the blank lines by hand to make the results easier to read.
Because the query has no ORDER BY clause, the results are listed in the order that the new nodes were met. This is why they come in groups where each next group has a path length that’s one step longer than the lengths of the paths in the previous group. You should consider the within-group ordering to be unpredictable. Of course, and as usual, you should write an ORDER BY clause to ask for the ordering that you want.
This picture shows you each of the fourteen paths in groups of increasing path length corresponding to the ysqlsh output.
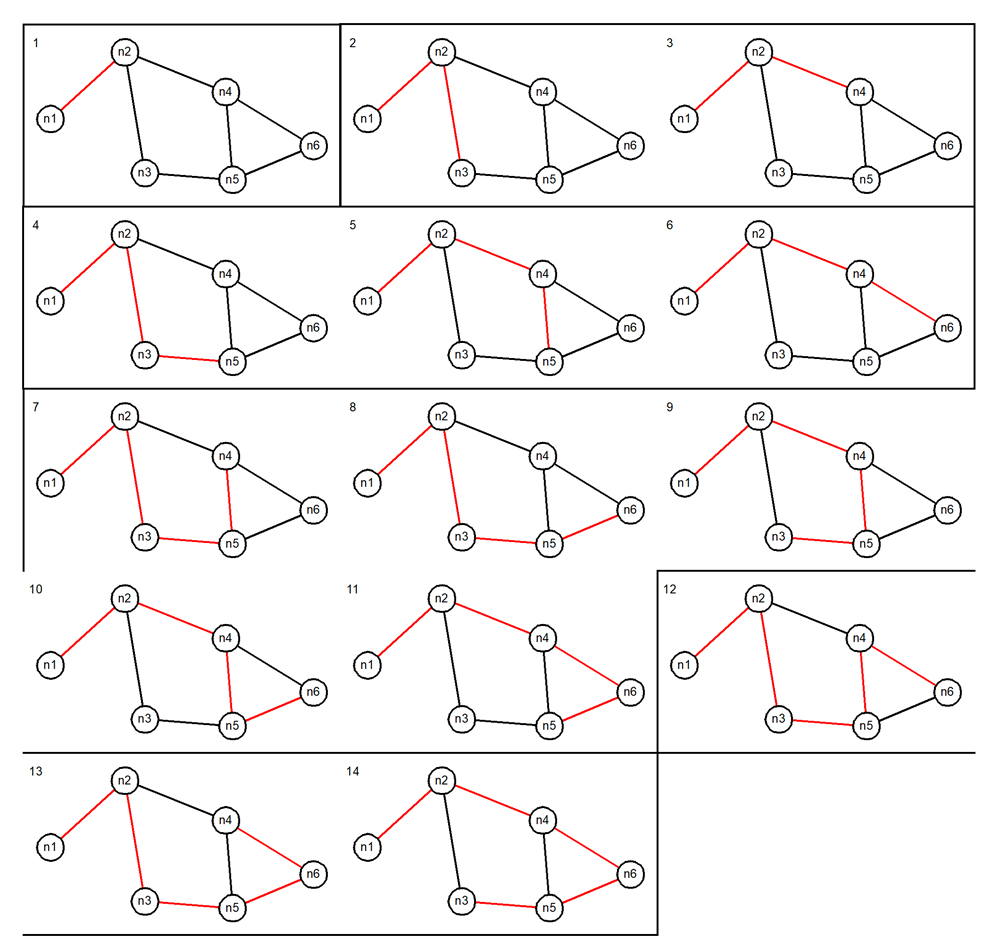
With this picture before you, you can readily appreciate the following general properties of the algorithm that the undirected cyclic graph path-finding recursive CTE expresses:
- The algorithm produces a set, in the strict mathematical sense of the term: there are no duplicate members.
- A longer path may completely contain a shorter path. (Of course, the containing path is still different from the path that it contains.)
- A path never backtracks immediately to the node that it just came from.
- A path never returns, no matter how roundabout the route might be, to any node that the path contains. Rather, it always stops one step short of this.
- There can be many paths to the same node. Generally, some will be longer than others, but they might all be the same length. Such paths might well have several nodes in common. You can see this with these paths to “n5”:#4: n1 > n2 > n3 > n5
#5: n1 > n2 > n4 > n5
#11: n1 > n2 > n4 > n6 > n5
These properties are exactly what are required to meet the goal of finding every distinct path, from the starting node, to every other reachable node. (I’ll return to the topic of containment presently). I said this in Part One—and I’ll say it again now: even now, after a few decades of using SQL every working day, I’m astonished by the power of declarative SQL. Here’s the SQL that I showed you above, written with the bare minimum of whitespace. It seems to me still to be perfectly readable—at least once you’ve internalized the essential background understanding.
with recursive paths(path) as ( select array['n1', node_2] from edges where node_1 = 'n1' union all select p.path||e.node_2 from edges e inner join paths p on e.node_1 = p.path[cardinality(path)] where not e.node_2 = any(p.path)) select path from paths;
It’s just thirty-eight words. And it fits comfortably in a tweet!
The SQL is encapsulated for ease of reuse in the procedure “find_paths()” created by the script cr-find-paths-with-nocycle-check.sql. It has a single formal parameter “seed”—the node from which to find the paths to the other nodes.
Finding the shortest paths and the unique containing paths
The approach described above that finds the paths in an undirected cyclic graph finds every single distinct path in the graph under analysis. As mentioned, it’s possible that several different paths from a given start node all reach the same node. Moreover, any one path that steps two or more nodes from the starting node contains the shorter paths from that starting node to each of the nodes that define it. Consider the paths “n1 > n2” and “n1 > n2 > n3”. These are clearly distinct. But you can infer the existence of the shorter path from the longer one because the latter contains the former. Take what I just wrote to be the definition of containment in this context. To solve the Bacon Numbers problem, you need only the shortest path to every reachable node—or, more carefully stated, an arbitrarily chosen path from the set of shortest paths to every reachable node. And sometimes, it’s useful to list only the unique containing paths for the set of shortest paths to bring the answer in the maximally compact form by avoiding redundancy.
Note: The PostgreSQL documentation of array functionality names the @> operator the “contains” operator. It determines if one array contains another. YugabyteDB inherits the operator and the YSQL documentation inherits the vocabulary.
I decided to use a building-block approach where the path-finding code inserts the paths that it finds (with no ORDER BY, of course) into a table. Then other procedures read from, and write to, tables with the same structure whose names you specify. Naturally, these procedures use dynamic SQL.
The procedure “restrict_to_shortest_paths()” does what its name says, reading from a table that holds all distinct paths. The script cr-restrict-to-shortest-paths.sql creates this procedure. The procedure “restrict_to_unq_containing_paths()”, created by the script cr-restrict-to-unq-containing-paths.sql, finds the unique containing paths from a table that holds distinct paths of interest. Each of these procedures has an “in_tab” and an “out_tab” formal parameter. Of course, there’s a “list_paths()” table function with a single formal parameter “tab”.
Notice how the array “contains” operator @> is used to determine if a putative containing path does indeed constain another path of interest. Yet again, “array” functionality comes to the rescue!
I’ll show you these procedures in action in the next section.
Applying the use-case-agnostic path-finding approach to IMDb data
The IMDb data set that I used, curated by Oberlin College Computer Science Department for the assignment “Everything is better with Bacon” is too big to allow graphic representation. So I’ll show you the complete analysis first on synthetic data with just a few actors and movies. Then I’ll show just some sample results from the analysis of real IMDb data.
Solving the Bacon Numbers problem for synthetic data
I’ll summarize the section Computing Bacon Numbers for a small set of synthetic actors and movies data here. The IMDb represents its facts in an obvious, straightforward, way. Here’s the entity-relationship diagram:
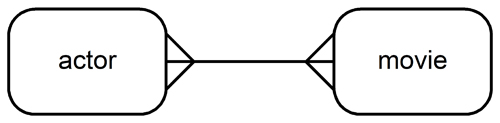
- each actor must act in at least one movie
- each movie’s cast must list at least one actor
This implies an “actors” table, a “movies” table, and a “cast_members” intersection table. It’s easy to use this starting point to populate the “edges” table (with columns “node_1” and “node_2”) just like the code discussed in the previous sections uses—and with a “movies” column of data type text[] that holds the list of movies that brought the edge between the two actors, again as explained in the previous sections.
Here is what the data that the present section uses looks like:
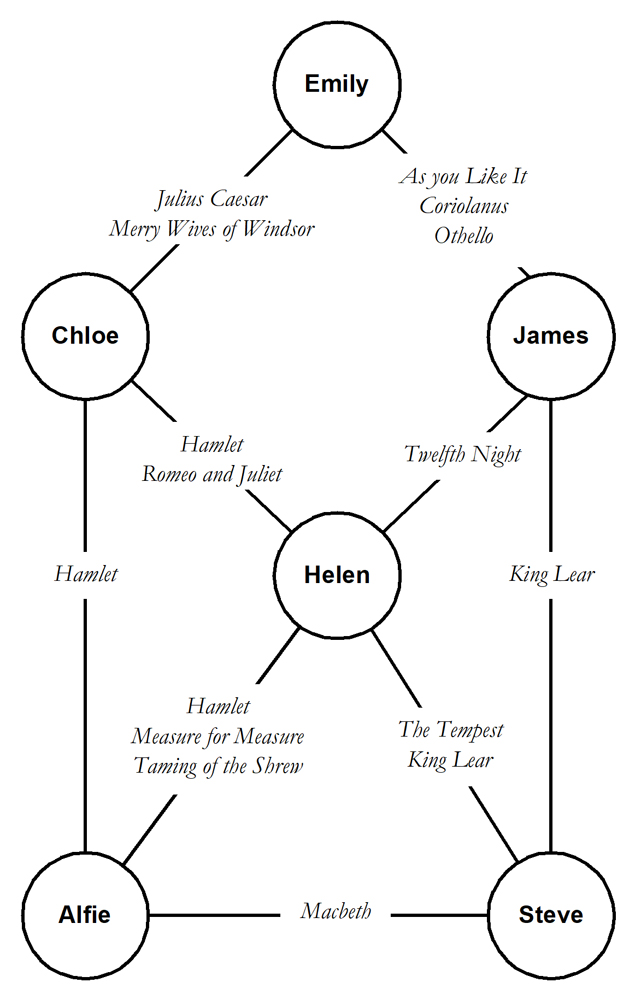
And here is the picture that the naïve “find_paths()” procedure, followed by the “restrict_to_shortest_paths()” procedure, followed by the “list_paths()” table function produces. I said “naïve” because that approach produces all the paths and only then prunes down the result set to just the shortest ones. I’ll explain in the next section that this won’t work on data sets with a serious size. Rather, you have to implement early pruning. The data set is small enough that you can fairly easily convince yourself that the picture is correct:
- There’s a path from the starting node “Emily” to each of the other five nodes.
- While you can find other paths with the same length to some of these nodes, you can’t find any shorter ones.
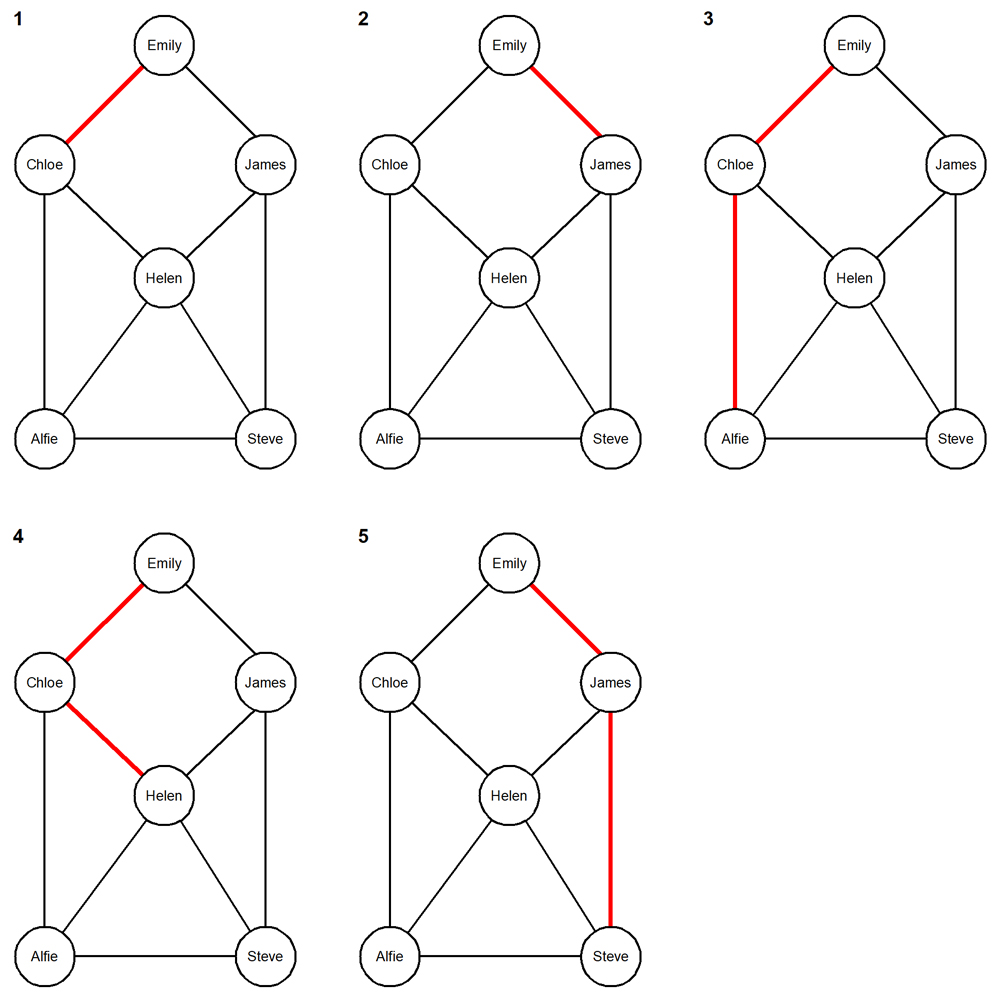
The YSQL documentation that describes the synthetic data exercise goes on to decorate each edge with the list of movies that brought it. I’ll show you this on real IMDb data in the next section.
You might like to run the “restrict_to_unq_containing_paths()” procedure on the results from “restrict_to_shortest_paths()” and then look at what this produces with “list_paths()”. It slims down the result set to just three paths:
path ---- Emily > Chloe > Alfie Emily > Chloe > Helen Emily > James > Steve
Solving the Bacon Numbers problem for real IMDb data
I’ll summarize the section Computing Bacon Numbers for real IMDb data here. The starting point is the data set imdb.small.txt—a 1817 line file with just 161 fully connected actors provided by the Oberlin College Computer Science department. Here are a few lines from the file:
... Alec Guinness|Kind Hearts and Coronets (1949) Alec Guinness|Ladykillers, The (1955) Alec Guinness|Last Holiday (1950) Alec Guinness|Lavender Hill Mob, The (1951) Alec Guinness|Lawrence of Arabia (1962) Alec Guinness|Little Dorrit (1988) Alec Guinness|Lovesick (1983) ...
It’s very easy to use the \copy metacommand at the ysqlsh prompt to ingest this file directly into the “cast_members” table:
\copy cast_members(actor, movie) from 'imdb-small.txt' with delimiter '|';
For completeness, a post-processing step then populates the “actors” and “movies” tables and creates the foreign keys—but the path finding procedure doesn’t need this. You can then immediately apply the exact same processing to this data that I explained for the synthetic data set. But beware, the “find_paths()” procedure will run for a very long time before crashing gracelessly with one of a few possible “out of resource” errors. At least, this is the case on a software engineer’s ordinary high-end laptop. You’ll get this outcome both with PostgreSQL and YugabyteDB. I made no attempt to tune the relevant resource-controlling parameters because I’d seen enough to know that the naïve “find_paths()” implementation is simply not up to the task.
My old friend Jonathan Lewis is well known for a nice visual metaphor for the problem: the brontosaurus query.
He writes about this in the conference paper “Just Don’t Do It—Sins of omission and commission”, which you can download here. Look at slide #23 and what follows. His point is that the silhouette of the brontosaurus’s body reminds you of this:
- if you find that you’ve written a
SELECTstatement whose input is a modestly sized data set, and whose final result set is quite small
- and if, during its execution, it produces an enormous intermediate result set
- then you’ve got an awful query and you need to find some way to prune that intermediate set before it ever starts to grow.
I won’t attempt to explain the early pruning approach that I invented here because it’s all in the YSQL documentation. See especially the sections Pseudocode definition of the semantics (of the recursive CTE), PL/pgSQL procedure implementation of the pseudocode, and How to implement early path pruning. I examine the performance characteristics, and I reason about the intermediate result set sizes, in the section Stress testing different find_paths() implementations on maximally connected graphs. This compares the naïve “find_paths()” implementation with the one that implements early pruning.
Suffice it to say here that, using the early pruning implementation, a single-node YugabyteDB cluster on my high-end MacBook finds the 160 paths from Kevin Bacon to each of the other 161 actors in something like five seconds. (It’s faster if you use PostgreSQL because a monolithic SQL database is inevitably faster than a distributed one.) By construction, these paths are already the shortest paths.
Note: the code zip that I mentioned at the start of this post includes a little timing utility exposed as the procedure “start_stopwatch()” and the function “stopwatch_reading()”. It formats the output for readability in the same way that the output following the \timing on metacommand does. But it has the advantage that the elapsed wall clock time is reported only when you ask for this and that, because you read the clock using SELECT, the answer goes properly to the spool file—where you want it.
Having populated a table with these 160 paths, the “decorated_paths_report()” table function finishes very quickly. The script cr-decorated-paths-report.sql creates it. The first mandatory formal parameter “tab” names the table where the paths are; and the second optional parameter “terminal” lets you specify a single actor of interest (Al Pacino in the example output below). If you don’t provide an actual value for this, then the report shows every decorated path. Here is the output that I showed at the start of this post.
Kevin Bacon She's Having a Baby Wild Things Bill Murray Saturday Night Live: Game Show Parodies Billy Crystal Muhammad Ali: Through the Eyes of the World James Earl Jones Looking for Richard Al Pacino
Problem solved!
Conclusion
The Bacon Numbers problem is a set-piece study and assignment for university students of computer science. This reflects the fact that the algorithm design, and the subsequent implementation, using ordinary “if-then-else” programming, are significant challenges for would-be programmers at this level. At the risk of repeating myself, I have to say that it’s astonishing that with only a reasonable understanding of SQL, and then some dedicated study of the recursive CTE, you can write down the essence of the solution in a tweet! Admittedly, you then have to think more—and, in my case, wait for the software engineering muse to visit—so that you can implement early pruning. But once somebody has shown you the trick, as I’ve now shown you, it’s not at all hard to understand.
It’s also remarkable that all this power is available to you in a modern, cloud native, open source, distributed SQL database!
You’ll have noticed how the implementation of the Bacon Numbers solution made heavy use of YSQL’s “array” functionality, inherited, of course, from PostgreSQL and documented in the section Array data types and functionality. This functionality turns out to be invaluable in many situations. But without prior understanding, you’re unlikely to spot, when you’re solving a new problem, what you should now study so that you can write the optimal solution. I therefore strongly recommend setting aside time to study array functionality.
So… go ahead and enjoy. Happy recursive CTE programming!


